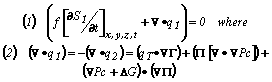
Revisiting The Buckley-Leverett Question Again
(An Overview of a Proposed GRC/2004 Poster Presentation)1
By Walter Rose2
ABSTRACT
Like the writings of many Authors1 to 21 during the 20th Century3, some less-remembered ones to be recalled here in the presentation of the Poster Presentation mentioned in the first footnote below, are in a series of papers published by Rose and collaborators (1951 et seq.)22 to 47 where both parallel and perpendicular attempts also were being made again and again. The aim, of course, was (and indeed still is!) to simplify, upgrade and extend the utility of vintage Buckley-Leverett algorithms (1942)25 so that at least partial proof of the proposed revisions could be confidentially employed as useful algorithms for productively modeling certain multiphase porous media transport processes. In particular, the cases to be considered are those where explicit account of classical coupling phenomena needs to be properly applied. This means that attention is being given to all low intensity irreversible processes where linearity between thermodynamic measurements involving conjugate macroscopically observed fluxes and forces on the one side, and between thermostatic measurements of displacements and equilibrium forces on the other. While many perplexing (indeed critical) issues still remain unresolved, the reader should not expect any of them to be fully illuminated by anything that will be displayed in any of the disclosures made during this Poster Presentation. After all, it has been generally conceded that for more than a Century the full proof of the underlying Darcian-based Buckley-Leverett dogma will not be available until coherent experimental proof of at least one of the many postulated theories that have appeared in the published literature so far has been fully confirmed. What will be found, however, in what follows is a new way to slightly (but perhaps significantly) rephrase a very old question. In particular, upon accepting equations that appear in Rose (1988)11 and at many other locations, we simply give a verbal and equivalent analytical algorithm as a sensible way for future workers (particularly gifted modern experimentalists) to confirm an ad-hoc theoretical to model two-phase, isothermal. and low-intensity flow of immiscible Newtonian fluid pairs in homogeneous and isotropic consolidated water-wet porous rock samples that are perturbed because of superimposed viscous coupling and spontaneous capillary imbibition effects.
KEY WORDS
porous media, transport process modeling, classical Buckley-Leverett. two-phase systems, viscous coupling, spontaneous capillary imbibition.
THEORETICAL BACKGROUND
As in Rose1 we start with the obvious but ingenious conservation of mass and Darcy-based statements which is where Buckley & Leverett2 left things some 60 years ago … as indeed many modern authorities also do as a way to utilize the simpler Darcian-based formulations. 3 Thus, without apology we write:
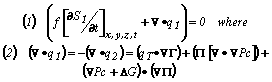


LITERATURE CITATIONS
Some 20th Century Writings About Porous Media Transport Phenomena
1 E. Buckingham (1907), "Studies in the Movement of Soil Moisture", U.S.Department of Agriculture, Bureau of Soils, Bulletin 28,
2 L. A. Richards (1931), "Capillary Conduction of Liquids through Porous Media", Physics, 1: 318-333.
3 M. Muskat (1937), The Flow of Homogeneous Fluids Through Porous Media; cf. also Muskat (1949), Physical Principles of Oil Production, both being McGraw-Hill Books (New York).
4 M. K. Hubbert (1940), "Theory of Ground Water Motion", Journal of Geology, 48: 785-044: see also in (1956), "Darcy Law and the Field Equations of the flow of underground fluids", Transactions AIME, 207: 222-239; and see below reference to the Deffeyes (2001) .
5 S. E. Buckley and M. C. Leverett (1942), "Mechanism of Fluid Displacement in Sands", Transactions AIME, 146: 107-116.
6 A. E. Scheidegger (1957), The Physics of Flow through Porous Media, University of Toronto Press; see (1960) and (1974) for the 2nd and 3rd Editions of this one of his many relevant monographs.
7 M. Tribus (1961), Thermostatics and Thermodynamics (D. Van Nostrand (especially see Chapter 15, p. 519 ff.).
8 S. R. DeGroot and P. Mazur (1962), Non-Equilibrium Thermodynamics, for an overview of Onsager's Nobel Prize awardwed work (North-Holland Publishing Company. Amsterdam).
9 J. Bear (1972), Dynamics of Fluids in Porous Media, American Elsevier (New York); also see later the J. Bear & Y. Bachmat (1990), Introduction to Modeling of Transport Phenomena in Porous Media, cf. §5.3.5 in particular, (Kluwer Academic Publishers).
10 C. Marle (1981) in Multiphase Flow in Porous Media, (Gulf Publishing Company).
11 F. A. L. Dullien (1992a) in Porous Media: Fluid Transfer and Pore Structure, 2nd Edition, (Academic Press. New York)
12 F. Siddiqui and Larry Lake (1992b), "A Dynamic Theory of Hydrocarbon Migration", Mathematical Geology 24: 305-328.
13 Zarcone & Lenormand (1994), "Determination experimentale de couplage visqueux dans les ecoulements diphasiques en Milieu poreux", C. R. Acad. Sci. Paris Serie II , 1429-1438.
14 Dullien & Dong (1995) "Experimental Determination of the Flow Transport Coefficients in the Coupled Equations of Two-phase Flow in Porous Media", Transport in Porous Media, 25: 97-120.
15 M. Kaviany (1995) in Principles of Heat Transfer in Porous Media. 2nd Edition, (Springer Verlag. Berlin).
16 A. Hadad, J. Benbat, H. Rubin (1996), "Simulation of Immiscible Multiphase Flow in Porous Media. A Focus on the Capillary Fringe" in Transport in Porous Media, 12: 229-240.
17 A. Babchin and J-. Y. Yuan (1997), "On the capillary coupling between two phases n a Droplet rain Model", Transport in Porous Media, 26: 226-228.
18 Ayub, Muhammad and Bentsen, Ramon, (1999), “Interfacial viscous coupling: a myth or reality?”, Journal of Petroleum Science & Engineering, 23: 13-26.
19 Bentsen, R. G. (2001), “The Physical Origin of Interfacial Coupling in 2-Phase Flow in Porous Media”, Transport in Porous Media, 44: 109-122./
20 K. S. Deffeyes (2001), Hubbert's Peak, The Impending World Oil Shortags, cf. especially page 201 for his discussion where a deivation is given for Hubberrt's use if the 'logiatic equation' firasgt employed in 1838 by Verlust in his analysis of Malthus's famous unlimited population growth theory in Corr. Math. et Phys.,10: 113.
21 R. Byron Bird, Warren Stewart, Edwin Lightfootl (2002) Tr/ansport Phenomena, cf. 2nd Edition in (2002), Wiley, New York.
Some Post-1950 to Date Papers by W. Rose & Collaborators
22 W. Rose (1951). "Some problems of Relative Permeability Measurement", Proceedings of the 3rd World Petoleum Congress, II: 446-459, this being a companion paper to the one presented by Yuster at the same conference.
23 W. Rose and P. H. Scott (1953), "An Explanation of the Yusteerr Effect", Journal of Petroleum Technology, 4: 19-20; see also W. Rose (1960), "Effect of Fluid/Fluid Interfacial Boundary Condition in Affecting Multiphase Fluid Flow", Illinois State Geologic Survey, Circular 291 (19 pages).
24 W. Rose and R. Heins (1962), "Moving Iterfaces and Contact Angle Rate-Dependentcy", Jounal of Colloid Science, 17: 39-48; cf. Rose (1961),"Fluid/Fluid Interfaees in Steady Motion", Nature, 191, 242=243.
25 W. Rose (1963). "Aspects des Processus de Mouillage dans les Solides Poreaux" in l'Institut Française du Petrole. XVIII: 1571-1590.
26 W. Rose (1966), "Reservoir Engineering, Reformulated" in the Bulletin of the Penn State Engineering Experiment Station, Circular 71: 23-68.
27 W. Rose (1969), "Transport through Interstitial Paths of Porous Solids", METU (Turkey) Journal of Pure & Applied Science, 2: 117-132.
28 W. Rose (1972), "Reservoir Engineering at the Crossroads. Ways of Thinking and Ways of Doing", Bulletin of the Iranian Petroleum Institute, 46: 23-27; see also 17 W. Rose (1974), "Second Thoughts on Darcy's Law", ibid, 48: 25-30.
29 W. Rose (1976), "Darcy's Law Revisited (cf. especially Appendix therein)", Journal of Mining Geology (Nigeria), 13: 38-44.
30 W. Rose & R. Gallegos (19-23 Matzo 1979 ), "Measuring Relative Permeabilities for Estimating Reserves", Procedimiento Panamericano de Ingenieria del Petroleo, Mexico, Abstract in Programa Technico.
31 W. Rose (1987), "Relative Permeability", SPE Handbook Of Petroleum Engineering, Chapter 28 (25 pages).
32 W. Rose, (1988), "Attaching new meanings to the Equations of Buckley and Leverett", Journal of Petroleum Science & Engineering, 1: 223-228.
33 W. Rose (1990a), Lagrangian Simulation of Coupled Two-phase Flows", Mathematical Geology, 22: 641-654.
34 W. Rose (1990b), "Optimising Experimental Design for Coupled Porous Media Flow Studies", Experimental Thermal & Fluid Science, 3:613-532.
35 W. Rose (1991a), "Richards Assumptions and Hassler's Presumptions", Transport in Porous Media, 6: 91-99.
36 W. Rose (1991b), "Critical questions about the coupling hypothesis", Journal of Petroleum Science & Engineering, 5: 299-307.
37 W. Rose (1995a), "Ideas about Viscous Coupling in Anisotropic Media", Transport in Porous Media, 18: 87-93; cf.
38 W. Rose (1995b), "Generalized Description of Multiphase Flow in Anisotropic Porous Media", Proceedings 32nd Annual Tevhnical Meeting of the Society of Engineering Sciences Abstract, pp. 483- 489.
39 W. Rose (1996), "Letter to the Editor of TiPM", Transport in Porous Media, 22: 359-360.
40 W. Rose, A. Babchin & J. Y. Yuan (1999a). "Coupled Transport in and through Fractured Rocks", Proceedings Lawrence Berkeley National Laboratory, #42717, Extended Abstract pp, 210-223.
41 W. Rose (1999b), "Relative Permeability Ideas … Then and Now", buried in the Proceedings of the SPE Eastern Division Regional Meeting, SPE Paper 42718, pages 115-141.
42 W. Rose (2000a), ” A Commentary on the Bartley/Ruth paper", Transport in Porous Media, 40: 355-358.
43 W. Rose (2000b), "Myths About Later-day Extensions of Darcy's Law", in J. of Petroleum Science & Engineering, 26: 187-198.
44 M. Asadi, Ali Ghalambor, M. K. Shirazi & W. Rose (2000c), "Anisotropic Permeability Measurement fo Coupled Systems, Proceedings SPE Asian- Pacific Conference on Integrated Modeling for
Asset Management, Yokohoma, Japan, SPE Paper 59396.
45 W. Rose (2001a), "Modeling Forced versus Spontaneous Capillary Imbibition Processes Commonly Occurring in Porous Sediments", Journal Of Petroleum Science & Engineering, 30: 155-166.
46 W. Rose (2001b), "Theory of Spontaneous versus Induced Capillary Imbibition", Transport in Porous Media, Technical Note 44: 591-598.
47 W. Rose and Derek Robinson (2003, in press), "Transport Processes in Fluid-saturated Porous Media" in a Letter-to-the-Editor format, Transport in Porous Media.
Unsaturated Flow:
Hassanizadeh, S.M., M.A. Celia, and H.K. Dahle, "Dynamic effects in the capillary pressure-saturation relationship and their impacts on unsaturated flow," Vadose Zone Journal, 1, pp. 38-57, 2002.
********************
Density-dependent Flow and Transport:
Watson, S.J., D.A. Barry, R.J. Schotting, and S.M. Hassanizadeh, "Validation of classical density-dependent solute transport theory for stable, high-concentration brine displacements in coarse and medium sands," Advances in Water Resources, 25, pp. 611-635, 2002.
Watson, S.J., D.A. Barry, R.J. Schotting, and S.M. Hassanizadeh, "On the validity of Darcy's Law for stable high-concentration displacements in granular porous media," Transport in Porous Media, 47, 149-167, 2002.
********************************
Virus Transport
Schijven, J.F. and Hassanizadeh, S.M., "Virus removal by soil passage at filed scale and groundwater protection of sandy aquifers", Water Sci. Tech., 46 pp 123-129, 2002
Schijven J.F., de Bruin H.A.M., Hassanizadeh, S.M., Roda Husman A.M. de, "Bacteriophages and clostridium spores as indicator organisms for removal of pathogens by passage through saturated dune sand." Water Res., pp. 2186-2194, 2003.
Schijven, J.F., S.M. Hassanizadeh, R.A.H.M. de Bruin, "Two-site kinetic modeling of bacteriophage transport through columns of saturated dune sand," Journal of Contaminant Hydrology, 57, pp 259-279, 2002.
Schijven, J.F. , R.A.H.M. de Bruin, S.M. Hassanizadeh, "Column experiments for evaluating field data on removal rates of bacteriophages by passage through saturated dune sand," Journal of Contaminant Hydrology, 58, pp. 243-259, 2002.
Schijven, J.F., G. Medema, A.J. Vogelaar, and S.M. Hassanizadeh, "Removal of microorganisms by deep well injection," J. Contam. Hydrol., 44, pp. 301-327, 2000.
Schijven, J.F., S.M. Hassanizadeh, S.E. Dowd, and S.D. Pillai, "Modeling virus adsorption in batch and column experiments," Quantitative Microbiology, 2, pp. 5-20, 2000.
Schijven, J.F.and S.M. Hassanizadeh, "Removal of viruses by soil passage: overview of modeling, processes and parameters," Critical Rev. Env. Sci. Tech., 30, 49-127, 2000.
Schijven, J.F., G. Medema, and S.M. Hassanizadeh "Virusverwijdering door kunstmatige infiltratie: Veilig ontwerp" (in Dutch; Removal of viruses by artificial recharge: A safe design), H2O, 34, no. 6, pp. 28-30, 2001.
Schijven, J.F., S.M. Hassanizadeh, "Calculation of zone of protection of drinking water wells against microbial pollution," In: J.N. Bandyopandhyay and D.Nagesh Kumar (eds.), Proceedings of the Int'l Conf. on Advances in Civil Engineering, 3-5 January 2002, Kharagpur, India, Allied Publ. Limited, New Delhi, pp. 11-20, 2002.
Schijven, J.F., S.M. Hassanizadeh, "Calculation of zone of protection of drinking water wells against microbial pollution," In: J.N. Bandyopandhyay and D.Nagesh Kumar (eds.), Proceedings of the Int'l Conf. on Advances in Civil Engineering, 3-5 January 2002, Kharagpur, India, Allied Publ. Limited, New Delhi, pp. 11-20, 2002.
Schijven, J.F., S.M. Hassanizadeh, "Virus removal by soil passage at field scale," In: Tenth Biennial Symposium on Artifical Recharge of Groundwater, Tucson, Arizona, June 7-9 2001, pp. 191-200, 2001.
Schijven, J.F., S.M. Hassanizadeh, "Modeling of virus transport and removal in the subsurface," The Encyclopedia of Environmental Microbiology (Chief-Editor Gabriel Bitton, John Wiley & Sons, Inc, USA.), 2094-2107, 2002.
J.F. Schijven and S.M.
Hassanizadeh, "An overview of modelling removal of
viruses by soil passage," Proceedings of Future Groundwater
Resources at Risk, Changchun, P.R. China, 14-16 July 1998, UNESCO
Technical Documents in Hydrology No. 27, UNSECO, Paris, pp 56-69,
2000. Hassanizadeh, S.M.,
J.F Schijven, "Use of bacteriophages as tracers for the study of
removal of viruses," in: Tracers and Modeling in Hydrogeology,
ed. A. Dassargues (Proceedings of TRAM'2000 held in Liege, Belgium,
23-26 May 2000), pp. 167-174, 2000.
*****************************************
Basic Theories of Flow and Transport:
Hassanizadeh, S.M., M.A. Celia, and H.K. Dahle, "Dynamic effect in the capillary pressure-saturation relationship and its impacts on unsaturated flow," Agricultural Sciences, 7, pp. 69-71, 2002.
Hassanizadeh, S.M., M.A. Celia, and H.K. Dahle, "Dynamic effects in the capillary pressure-saturation relationship and their impacts on unsaturated flow," Vadose Zone Journal, 1, pp. 38-57, 2002.
Murdoch, A.I. and S.M. Hassanizadeh, "Macroscale balance relations for bulk, interfacial, and common line systems in multiphase flows through porous media on the basis of molecular considerations," International Journal of Multiphase Flow, 28, pp. 1091-1123, 2002.
Beliaev, A.Y. and S.M. Hassanizadeh, "A Theoretical Model of Hysteresis and Dynamic Effects in the Capillary Relation for Two-phase Flow in Porous Media," Transport in Porous Media, 43, pp. 487-510, 2001.
*********************************
Upscaling Multiphase flow in Porous Media:
Ataie-Ashtiani, B., S.M. Hassanizadeh, O. Oung, F.A. Weststrate, and A. Bezuijen, "Numerical modelling of two-phase flow in a geocentrifuge," Environmental
Ataie-Ashtiani, B., S.M. Hassanizadeh, and M.A. Celia, "Effects of heterogeneities on capillary pressure-saturation-relative permeability relationships," Journal of Contaminant Hydrology, 56, pp. 175-192, 2002. oAtaie-Ashtiani, B., S.M. Hassanizadeh, M. Oostrom, M.A. Celia, and M. White, "Effective parameters for two-phase flow in a porous medium with periodic heterogeneities," J. Contam. Hydrol., 49, 87-109, 2001.
Ataie-Ashtiani, B., S.M. Hassanizadeh, "Upscaling two-phase flow in porous media with randomly distributed microheterogeneities" in Computational Methods in Water Resources, Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder (Proceedings of CMWR2002, Delft, The Netherlands, June 23-28), pp. 1187-1194, 2002.
Ataie-Ashtiani, B., S.M. Hassanizadeh, O. Oung, F.A. Weststrate, A. Bezuijen, 'Numerical simulation of two-phase flow in a geocentrifuge' Computational Methods in Water Resources, Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder (Proceedings of CMWR2002, Delft, The Netherlands, June 23-28), pp. 225-232, 2002.
Ataie-Ashtiani, B., S.M. Hassanizadeh, M.A. Celia, M. Oostrom and M.D. White "Effective two-phase flow parameters for heterogeneous porous media," in: Computational Methods in Water Resources, ed. L.R. Bentley et al. (Proceedings of CMWR XIII, Calgary, Canada, June 25-29, 2000), 755-762, 2000.
Ataie-Ashtiani, B., S.M. Hassanizadeh, M. Oostrom and M.D. White, "Numerical simulation and homogenization of two-phase flow in heterogeneous porous media," in: Groundwater Updates, proceedings of the IAHR International Symposium on Groundwater, Sonic City, Japan, 8-10 May 2000, K. Sato and Y. Iwasa (eds.), Springer-Verlag, Tokyo, pp. 333-338, 2000.
******************************************************
Watershed Modeling:
Reggiani, P., M. Sivapalan, S.M. Hassanizadeh, and W.G. Gray, "Coupled equations for mass and momentum balance in a bifurcating stream channel network: Theoretical derivation and numerical implementation," Proceedings of the Royal Society (London) Series A: Mathematical, Physical & Engineering Sciences, Vol. 457, No. 2005, 157-189, 2001.
Reggiani, P., M. Sivapalan, and S.M. Hassanizadeh, "Conservation equations governing hillslope responses: Physical basis of water balance," Water Resour. Res., 36, 1845-1864, 2000.
*********************************************************
Solute Transport Modeling:
Leijnse, A., H. van de Weerd, and S.M. Hassanizadeh, "Modelling of uranium transport in Koongarra, Australia; The effect of a moving weathering zone," Mathematical Geology, 33, no. 1, pp. 1, 2001
**************************************************
Transport of radionuclides in porous media:
O Leijnse, A., H. van de Weerd, and S.M. Hassanizadeh, "Modelling of uranium transport in Koongarra, Australia; The effect of a moving weathering zone," Mathematical Geology, 33, no. 1, pp. 1, 2001.
************************************************
Multiphase Flow Modeling:
Hassanizadeh, S.M and W.G. Gray, "Mechanics and thermodynamics of multiphase flow in porous media including interphase boundaries," Adv. Water Resour., 13, 169-186, 1990.
Gallo C., S.M. Hassanizadeh, A.E. Rosenbom, and K.E.S. Klint, "NAPL migration in a fractured-till soil: the Ringe Site case (Denmark)"Computational Methods in Water Resources, Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder (Proceedings of CMWR2002, Delft, The Netherlands, June 23-28), pp. 655-662, 2002.
Dahle, H.K., M. A. Celia, S. M. Hassanizadeh, and K.H. Karlsen, 'A total pressure-saturation formulation of two-phase flow incorporating dynamic effects in the capillary-pressure-saturation relationship' Computational Methods in Water Resources, Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder (Proceedings of CMWR2002, Delft, The Netherlands, June 23-28), pp. 1067-1074, 2002.
Ataie-Ashtiani, B., S.M. Hassanizadeh, O. Oung, F.A. Weststrate, A. Bezuijen, 'Numerical simulation of two-phase flow in a geocentrifuge' Computational Methods in Water Resources, Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder (Proceedings of CMWR2002, Delft, The Netherlands, June 23-28), pp. 225-232, 2002.
Hassanizadeh, S.M. and Zhao Yongsheng, "Simulation of underground migration of NAPL," Proceedings of Future Groundwater Resources at Risk, Changchun, P.R. China, 14-16 July 1998, UNESCO Technical Documents in Hydrology No. 27, UNSECO, Paris, pp 225-228, 2000.
Koopmans, M.P., Hassanizadeh, M., Hofstee, C., Leijnse, A., Meurs, G. van, Taat, J., Timmerman, T., "Development of a Numerical Simulator for LNAPL weathering, Phase 1: P{reliminary Studies,"TNO-NITG-report, Netherlands Institute of Applied Geoscience TNO-NITG, 15 July 2002
********************************
Groundwater Flow Modeling:
Hassanizadeh, S.M., "Steady State Radial Flow into Wells in Stratified Aquifers", Agricultural Engineering Journal (in Persian), 2, June 1983.
I. Wemaere, Marivoet, J., Pitsch, H., Beaucaire, C., Marline, C., Michelot, J.-L., Phillipot, A.-C., Hassanizadeh, S.M., and van Weert, F., "The PHYMOL Project," in: Use of hydrogeological information in testing groundwater flow (Proceedings of Workshop on Site evaluation and design of experiments for radioactive waste disposal; Borgholm, Sweden, 1-3 September, 1997), Nuclear Energy Agency, ISBN 92-64-16153-8, pp. 347-353, 1999.
van Weert, F. and Hassanizadeh, S.M., "Supra-Regional Groundwater Modelling of the Northwest Euorpe over the Last 125000 Years," PHYMOL Project Technical Report, Report No. DOC RID/53/2000-EN, European Commission, Brussels, 86 pages, 2000.
Marivoet, J., van Keer, I., Wemaere, I., Ha*rdy, L., Pitsch, H., Beaucaire, C., Michelot, J.-L., Marlin, C., Phillipot, A.C., Hassanizadeh, S.M., and van Weert, F., "A Paleohydrogeological study of the Mol Site," PHYMOL Project Final Report, Report No. 19146EN, European Commission, Brussels, 101 pages, 2000.
*****************************************/
General Hydrology:
*********************************
Pore-scale network Modeling:
T. Gielen, S.M. Hassanizadeh, M.A. Celia, and H.K. Dahle, "Study of Pc-Sw relationships using a dynamic pore-scale network model,"Computational Methods in Water Resources, Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder (Proceedings of CMWR2002, Delft, The Netherlands, June 23-28), pp. 1099-1107, 2002.
Celia M.A., H.K. Dahle, and S.M. Hassanizadeh, "Dynamic pore-scale network models for two-phase flow in porous media," in: Computational Methods in Water Resources, ed. L.R. Bentley et al. (Proceedings of CMWR XIII, Calgary, Canada, June 25-29, 2000), 217-223, 2000
**********************************
Modeling Biodegradation of
Organic Contaminants:
Gallo C. and S.M. Hassanizadeh, Modeling NAPL dissolution and biodegradation interactions: effect of toxicity and biomass growth limitations' Computational Methods in Water Resources, Eds. S.M. Hassanizadeh, R.J. Schotting, W.G. Gray, and G.F. Pinder (Proceedings of CMWR2002, Delft, The Netherlands, June 23-28), pp. 859-866, 2002.
Bouw, L., S.M. Hassanizadeh, and A. Leijnse, "Multiphase flow and enhanced biodegradation of dense non-aqueous phase liquids: Experimental design" to appear in IAHS Red Book series, 2002.
Gallo, C. and S. M. Hassanizadeh, "Influence of biodegradation on NAPL flow and dissolution in groundwater," in: Computational Methods in Water Resources, ed. L.R. Bentley et al. (Proceedings of CMWR XIII, Calgary, Canada, June 25-29, 2000), 129-138, 2000
1 This manuscript is an abbreviated version of a much larger paper which since 11/15/2003 is being editorially peer reviewed for possible exclusive publication in Elsevier's Journal of Petroleum Science & Engineering, It is displayed here, however, to describe the subject of an off-the-record Poster Presentation which, if wanted, can be a poster part of the 2004 Gordon Research Conference of :"Flow & Transport in Permeable Media" that is scheduled to be chaired by Professor S. M. Hassanizadeh next July at Queen's College, Oxford, UK.
2 Contact Addresses for the Author Illini Technologists International, P. O. Box 2424, Champaign, Illinois 61825, USA, Facsimile: 1.217.358.9289; e-mail: wdrose@uiuc.edu.
3 Where for brevity only a few of the names of some of them like Buckingham (1907), to Richards (1931), to Muskat (1937) and (1949). to Hubbert (1940) and (1956), to Scheidegger (1951), Bear (1972) and Bear & Bachmat (1990)